"These variables form a hyperspace of possible designs, where each set of parameters uniquely defines a design of a nanophotonic structure with a certain optical property," Professor Yuebing Zheng at the University of Texas at Austin, tells Nanowerk. "Inverse design of nanophotonic devices is thus a task of searching this space for an optimal set of parameters that can produce the desired optical response."
Machine learning has emerged in the last few years as a powerful tool for sifting through this vast universe of possible design parameters to aid the design of nanophotonic devices tailored for specific applications.
However, machine learning techniques in nanotechnology are still in their infancy and suffer from a number of roadblocks towards practical real world application. One key challenge is the non-uniqueness problem, where any number of very different designs can produce nearly identical optical responses, which can significantly hurt the model's ability to learn.
Typically, machine learning algorithms train by using a data set of inputs linked with corresponding correct outputs. The goal of the training process is to continually update the algorithm to predict the correct answer as often as possible. In cases of high non-uniqueness, there are multiple correct answers for every input, and this can cause a lot of inaccuracies in the training process.
Various types of solutions have been previously proposed to address this non-uniqueness problem – like training a separate network for forward simulation in addition to the inverse model – but these can suffer from limitations, such as deterministic networks being unable to correct wrong predictions, and inaccuracies caused when the forward problem is difficult to model.
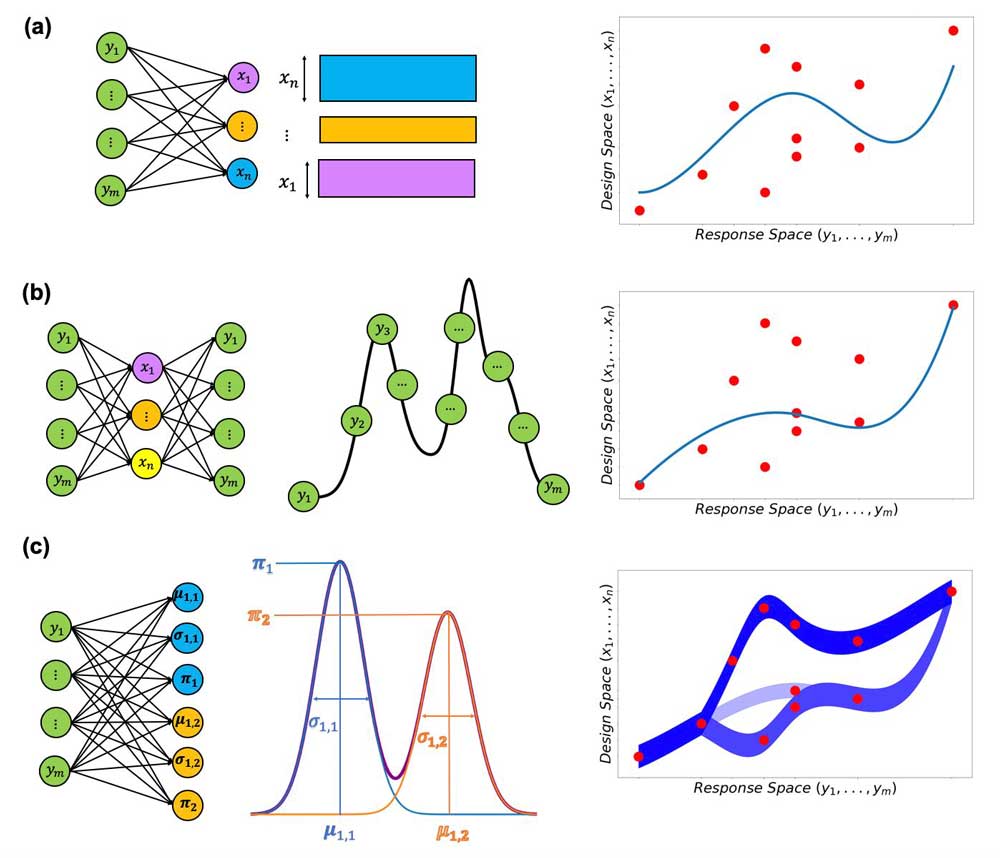
Different types of neural network (NN) models for solving the many-to-one problem. (a) A standard NN maps straight from the response (y1, …, ym) to the design (x1, …, xn). Attempting to learn a deterministic mapping can cause the model to try to predict in between degenerate solutions (red dots), and even prevent it from converging with unique solutions. (b) For the tandem network approach, the response is mapped to the design, which is connected to a pretrained and frozen modeling network that maps the design to the response. This can still have difficulty in converging, and an optimal solution may ignore other viable options. (c) A MDN produces a mixture of multiple Gaussian distributions for each design variable. Each distribution in the mixture is parametrized by a mean µ, a variance σ, and weight π. Probability distributions are represented by the shaded strips rather than a single line for deterministic mapping (right panels). The MDN can capture all degenerate solutions through multimodal distributions, with the relative strength of the modes visualized by the opacity (related to π) of each strip.
Zheng's group has demonstrated a novel approach that uses a type of neural network called a mixture density network – which models the designs as probability distributions rather than discrete values – to solve this non-uniqueness problem while also improving accuracy.
Mixture density networks (MDNs) are a type of neural network that have been around for a long time and for instance are applied to natural language processing.
"We are the first to propose using this type of architecture for inverse design and demonstrate that this can be a more robust solution to the non-uniqueness problem," Zheng says. "We also demonstrate our model on data sets that are far more complex than those typically used for machine-learning-based inverse design, both in terms of the degree of non-uniqueness, and the spectral complexity of the responses."
MDNs operate by modeling the final output as a probability distribution of possible values rather than single discrete values as with standard neural networks. They can theoretically capture any number of correct answers with multiple peaks in the distribution.
The team reports their findings in ACS Photonics ("A Deep Convolutional Mixture Density Network for Inverse Design of Layered Photonic Structures").
"The core working principle of the mixture density network compared to standard neural networks is that it predicts a probability distribution over all possible values rather than a single discrete deterministic prediction," Rohit Unni, the paper's co-first author, explains. "These distributions can then be sampled to yield a specific design, for example, by picking the point with the highest probability."
"The distributions can be any arbitrary shape so they can capture things like multiple correct answers, for example, with multiple peaks in the distribution, where each peak corresponds to a different unique solution," adds Kan Yao, who is the other co-first author. "The shape of the distribution, such as how wide the peaks are, can also give valuable information like the uncertainty of the prediction."
The fact that they are able to achieve good results despite the more difficult modeling task demonstrates the wide applicability of their model, as the team points out.
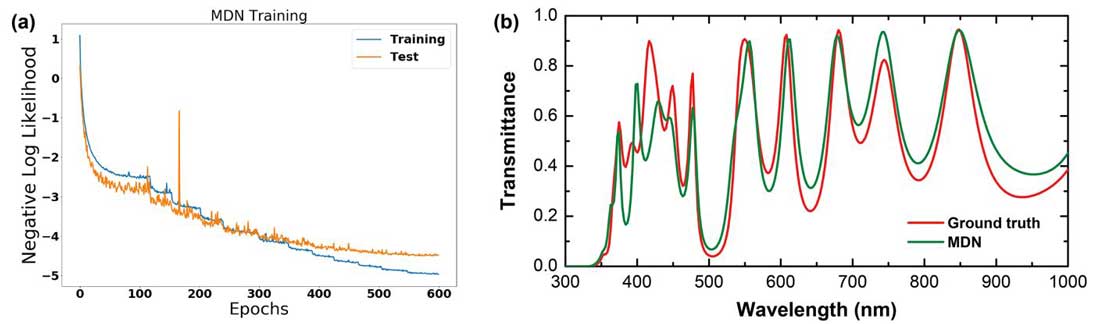
(a) Learning curve of the MDN trained for the 10-layer photonic structure for both the training and test data over 600 epochs, stopped early to prevent overfitting. The loss function minimized is the average negative log-likelihood. The test error is approximated from samples of the test data, which can occasionally cause large spikes due to sampling error. (b) Comparison of a requested spectrum (red curve) with the spectrum produced by the design suggested by the MDN model (green curve).
Neural networks have lots of possible configurations and parameters that can be tuned. The team cautions that their model is just a first step and the architecture can be further optimized before being applied to new data sets like metasurfaces and pattern-based structures.
In addition, the probabilistic nature of this model allows for a wide array of strategies of how to interpret the probability distribution to pick a given design. In their paper, the researchers present two simple strategies: simply taking the most likely point in each distribution; and an optimization-based method that involves sampling the distribution multiple times to find the best one.
"But we expect that further investigation, as well as incorporating other machine learning or conventional optimization techniques, can yield even more optimal strategies," says Unni.
The team hopes that the type of model they developed can be applied to designing a wide array of possible nanophotonic devices, including things like anti-reflective coatings, optical filters, and photonic crystals. They say that further refinement of machine learning based solutions can hopefully soon enable the creation of nanophotonic devices with capabilities beyond those possible with conventional design methods.
"One of the other biggest roadblocks to this field beyond this non-uniqueness problem is the difficulty in acquiring the training data," Zheng concludes. "We demonstrate our model on a type of structure where we can simulate large amounts of data quickly, but for most nanophotonic structures, running enough simulation to acquire the amount of data that is typically needed for machine learning algorithms is extremely computationally expensive. Some of the most valuable work in this field going forward would be addressing this concern, both with the availability of good quality benchmark data sets that other researchers can use to test new models quickly, and finding creative ways to reduce the amount of data needed in general."
Read the original article on Nanowerk.