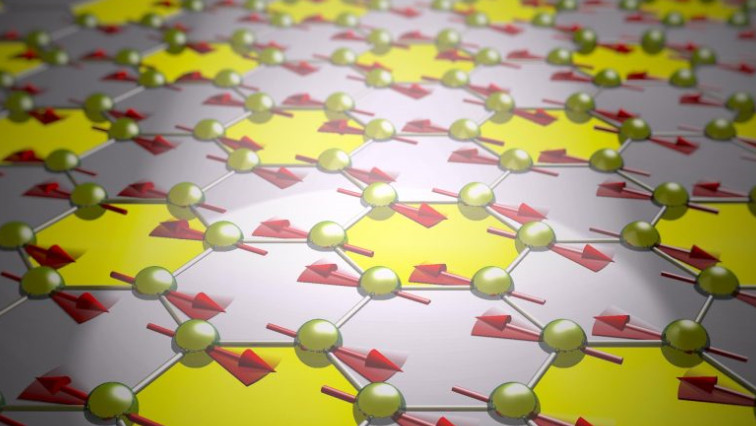
The thin atomic layers that make up van der Waals magnets may seem extremely fragile, but they can be about 200 times stronger than steel. Unfortunately, this mechanical strength does not necessarily translate into strong magnetic properties. The reason for this is that, in two dimensions, the magnetic order of these magnets becomes especially vulnerable to heat. Any temperature above the absolute zero (-273 °C) activates random fluctuations in the orientation of the microscopic spins, which can completely collapse the magnetic order. So until we can control their magnetic state, the promises of atomically thin magnets are just that: promises.
Controlling magnetism
The only way to counteract the thermal agitations is to stick magnetic spins more to some directions in the material than to others. Or, as physicists call it: to induce ‘magnetic anisotropy’. Doing so makes it harder for spins to change their orientation, thereby lifting their ordering temperature (known as the Curie temperature) way above absolute zero. Controlling anisotropy in low-dimensional magnets, in other words, paves a direct pathway to controlling their ordering temperature and thus the magnetism itself.
In their study the international team, which consisted of researchers from The Netherlands, Spain and Ukraine, used ultrashort pulses of light, a trillion times shorter than a single second, to induce the magnetic anisotropy in a two-dimensional van der Waals antiferromagnet. Why use light? “Because it’s a very convenient control knob”, Dr. Andrea Caviglia explains. “You can simply and swiftly turn it on and off and therefore manipulate the anisotropy on demand, which is exactly what we need if we want to start using these materials for efficient data storage.”
Tuning the color
By systematically varying the color of the light from visible to near-infrared, the scientists also found that not every type of light can generate magnetic anisotropy. To induce this property, the color of light needs to match the energy required to change the orbital state of the electron. That is to say: to change the way electron whirls around a positively charged nucleus. As the electron spin and its orbital motion are tightly linked, the light excitations induce anisotropy, which results in a two-dimensional spin-wave motion. “This motion is coherent – the whole spin ensemble moves in-phase at high frequencies”, says Jorrit Hortensius, a PhD student at TU Delft. “This is an elegant and at the same time virtually universal solution to manipulating magnetic anisotropy in practically any two-dimensional magnet.”
In this proof-of-principle experiment, the team showed that anisotropy can be photoinduced for a tiny fraction of time, nearly the same as the duration of the light pulse. However, for practical applications the changes to the magnet need to be sustained for a longer period of time. The scientists hope that light pulses with a longer-duration might help to reach this goal. Dr. Dmytro Afanasiev, who currently works at University of Regensburg says: “We hope that longer light pulses can even promote the magnetic order above the equilibrium ordering temperature, so that we can watch in real-time how the ordered state arises from magnetic chaos. This will certainly increase our understanding of magnetism in these van der Waals magnets.”
Read the original article on Delft University of Technology.