According to Huck Beng Chew and his doctoral student Yue Cui, materials, such as copper, are very different at these very small scales.
“Metals are typically polycrystalline in that they contain many grains,” Chew said. “Each grain is a single crystal structure where all the atoms are arranged neatly and very orderly. But the atomic structure of the boundary where these grains meet can be very complex and tend to have very high stresses.”
These grain boundary stresses are responsible for the fracture and fatigue properties of the metal, but until now, such detailed atomic-scale stress measurements were confined to molecular dynamics simulation models. Using data-driven approaches based on machine learning enables the study to quantify, for the first time, the grain boundary stresses in actual metal specimens imaged by electron microscopy.
“We used molecular dynamics simulations of copper grain boundaries to train our machine learning algorithm to recognize the arrangements of the atoms along the boundaries and identify patterns in the stress distributions within different grain boundary structures,” Cui said.
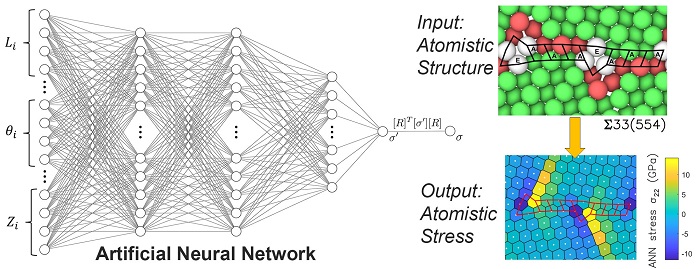
Left: Machine learning based on artificial neural networks as constitutive laws for atomic stress predictions. Right: Quantifying the local stress state of grain boundaries from atomic coordinate information
Eventually, the algorithm was able to predict very accurately the grain boundary stresses from both simulation and experimental image data with atomic-level resolution.
“We tested the accuracy of the machine learning algorithm with lots of different grain boundary structures until we were confident that the approach was reliable,” Cui said.
Cui said that the task was more challenging than they imagined, and they had to include physics-based constraints in their algorithms to achieve accurate predictions with limited training data.
“When you train the machine learning algorithm on specific grain boundaries, you will get extremely high accuracy in the stress predictions of these same boundaries,” Chew said, “but the more important question is, can the algorithm then predict the stress state of a new boundary that it has never seen before?”
Chew said, the answer is yes, and very well in fact.
“What machine learning does for the field of mechanics of materials is that it enables us to use data to make predictions quickly and autonomously. This is a significant advancement over the development of complicated and highly-specific physics-based models to make failure predictions,” Chew said.
Measuring these grain boundary stresses is the first step towards designing aerospace materials for extreme environment applications.
“Being able to establish quantitative descriptors of the boundaries will enable scientists to engineer grain boundaries to be stronger, and more heat and corrosion resistant,” Chew said.
Cui stressed that the algorithm they have developed is very general and can be used to quantify the atomic-scale stresses governing fracture and failure processes in many other material systems.
The study, “Machine-Learning Prediction of Atomistic Stress along Grain Boundaries,” by Yue Cui and Huck Beng Chew is published in Acta Materialia.
Read the original article on University of Illinois Board of Trustees.