 Strong force: Quantum computers could help astrophysicists simulate the behaviour of nuclei in the aftermath of the Big Bang. (Courtesy: iStock/vitacopS)
Strong force: Quantum computers could help astrophysicists simulate the behaviour of nuclei in the aftermath of the Big Bang. (Courtesy: iStock/vitacopS)
The strong nuclear force is what holds atomic nuclei together, and our current mathematical understanding of it has led to remarkable insights into the nature of matter. Still, certain questions – such as the matter composition of the very early universe – have eluded physicists’ best efforts, and computer simulations of these regimes are intrinsically limited even with the largest conceivable classical machines.
In light of these limitations, some physicists have turned to quantum computers, hoping that their capabilities are a better match for the requirements of the simulations. A joint team from the University of Waterloo and York University, both in Canada, has now made headway toward this goal by simulating the interactions between matter particles using a class of quantum algorithms known as variational algorithms. The work could make it possible to study the behaviour of nuclei in the aftermath of the Big Bang and in astrophysical objects such as neutron stars – systems that are inaccessible on classical computers.
Simulating fundamental forces
In the quantum theory of electromagnetic interactions (known as quantum electrodynamics, or QED), the particle that carries the electromagnetic force – the photon – does not directly interact with itself. This type of theory is known as an Abelian gauge theory. In contrast, the theory of the strong force (known as quantum chromodynamics, or QCD), is non-Abelian, and its force-carrying particles, called gluons, do interact with each other.
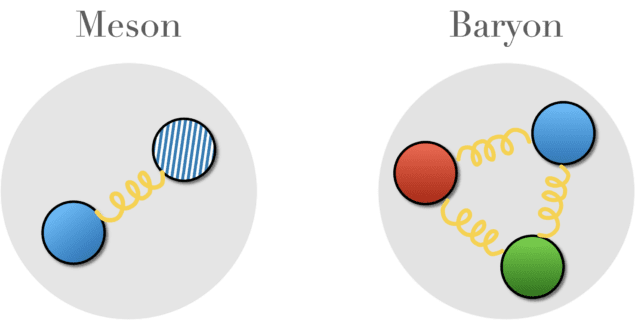 Composite particles: Artistic rendering of a meson (left) and baryon (right). The meson comprises a quark (represented by a filled circle), antiquark (represented by a striped circle), and a connecting gluon. The baryon consists of three quarks and three gluons. (Courtesy: Amara McCune and Jacob Marks)
Composite particles: Artistic rendering of a meson (left) and baryon (right). The meson comprises a quark (represented by a filled circle), antiquark (represented by a striped circle), and a connecting gluon. The baryon consists of three quarks and three gluons. (Courtesy: Amara McCune and Jacob Marks)
This interaction allows a rich variety of composite particles to form, including baryons like protons and neutrons, which are made up of three matter particles called quarks, and mesons, which are quark-antiquark pairs. “Non-Abelian gauge theories are at the basis of how the matter around us is formed, and are necessary for a full description of our universe,” explains Jinglei Zhang, a postdoctoral fellow at Waterloo and an author of a paper describing the recent quantum simulations.
While making predictions in QCD is critical to our understanding of our universe, it is not without its challenges. Due to the nature of the gluon interaction, only at the highest energies can quarks become freed from bonds with other quarks. This property, known as confinement, arises because the strength of the strong force increases with decreased energy. Unfortunately, this makes it unfeasible to calculate or even approximate particle processes using the mathematical methods typically applied in simpler theories such as QED.
Physicists must then adopt an alternative strategy: simulating quarks and gluons on a computer. But this approach also has limitations. While theoretical predictions are usually made assuming a continuous spacetime, like the one we think we live in, this is not possible on a computer. Instead, quarks must be constrained to points on a grid, separated by some fixed distance and connected by the force-carrying gluons.
This approach, which discretizes space, is known as lattice QCD. There are two frameworks for implementing it on a classical computer. The first framework discretizes time as well as space, which makes it impossible to simulate the system’s dynamics and introduces an obstacle known as the sign problem. This problem arises when calculating predictions for quarks and gluons at high energies, where the positive and negative contributions are nearly identical. The simulations then need to be incredibly precise to make accurate predictions. The second framework retains the continuous nature of time, but runs into a different problem: the time to generate predictions increases exponentially with the number of particles, restricting its applicability to relatively small systems.
Quantum computers may provide a solution. Within the continuous-time framework, the fact that quantum bits, or qubits, exist in a simultaneous superposition of multiple states frees quantum computers from the exponential scaling that plagues their classical counterparts. This freedom could, in principle, make it possible for physicists to extend lattice QCD to previously unapproachable regimes.
Computing with error-prone quantum processors
In practice, however, today’s quantum processors are relatively small in scale and limited in utility. This is primarily due to noise arising from interaction between the quantum computer and the surrounding environment. Fortunately, a class of quantum computational routines known as variational quantum algorithms is remarkably resilient to noise, enabling scientists to make use of these noisy, intermediate-scale quantum (NISQ) devices.
In variational quantum algorithms, a quantum processor works in concert with a classical processor to complete a task. As in other quantum algorithms, the quantum processor implements a sequence of gates that comprise a quantum circuit, and these gates act on a set of qubits called a register. The difference is that for variational quantum algorithms, some of these gates can be tuned by variable control parameters to generate a family of related quantum operations. Individual qubits, for example, can be controlled by “rotation angles”, which systematically transform qubit states into new superpositions of zero and one. The classical processor’s role, meanwhile, is to optimize over all of these parameters, choosing angles that allow the quantum processor to best perform the desired task.
 Best of both: In hybrid quantum-classical algorithms, quantum and classical computers work together as co-processors to complete a task. (Courtesy: Jinglei Zhang)
Best of both: In hybrid quantum-classical algorithms, quantum and classical computers work together as co-processors to complete a task. (Courtesy: Jinglei Zhang)
The first application of variational methods to quantum algorithms came in 2014 with the development of an algorithm known as the variational quantum eigensolver (VQE). In the VQE, the classical optimizer chooses rotation angles that transform the state of the register into a physical state of the model system being studied (an eigenstate). Using this technique, the algorithm’s developers were able to estimate the ground state energy of a molecule as precisely as they could with state-of-the-art classical techniques, despite the error-prone nature of their quantum processor. Since then, variational algorithms have been applied to a plethora of problems in chemistry and fundamental physics.
Lattice gauge theory on a quantum computer
In the latest work, which is described in Nature Communications, the Waterloo team showed for the first time that variational quantum algorithms enable NISQ processors to address questions in non-Abelian gauge theories. To demonstrate the feasibility of the technique, the researchers considered a lattice gauge theory model with the simplest possible non-Abelian group. While this model does not capture the full complexity of QCD, it retains some of the key features that make large-scale QCD simulations unfeasible on classical computers, and its matter particles and force-carriers behave like quarks and gluons respectively.
In the model, matter particles (fermions) and their antiparticles (antifermions) exist at fixed points along a one-dimensional chain, connected by gluon-like force-carriers. In the lowest-energy state of the model, fermions pair up with other fermions and antifermions pair with antifermions to form composite particles that resemble the baryons of QCD. The second-lowest energy state consists of fermion-antifermion pairs, which are analogous to mesons in QCD.
The team began by mapping the lattice of fermions and antifermions onto a system of quantum spins, which are easier to simulate on a quantum computer. Then, the researchers designed efficient variational quantum circuits to approximate the ground state and the first excited state of the model system. Because they knew the ground state and first excited state would be baryonic and mesonic respectively, they could restrict their variational searches to these smaller spaces, reducing overall computational cost.
To test the quality of this approach, the researchers ran their algorithms on an IBM quantum processor paired with a classical optimizer to estimate the energies of these two states for systems with up to four fermions and antifermions. These systems were small enough for the researchers to simulate them exactly on a classical computer, meaning they could compare the variational estimated energies with values extracted from the classical simulations. When they did, they found excellent agreement.
Read more

Quantum computer captures physics of high-energy particles
Building toward QCD
The Waterloo team’s findings mark a significant step toward a full-scale simulation of QCD on a quantum computer. The researchers now plan to extend their current method by adding more qubits, including three spatial dimensions, and enhancing the model to encompass the full nature of QCD. They also hope to push past the limits of lattice QCD on classical computers. “After that, we aim to simulate sign-problem afflicted models, including matter at high density and real-time dynamics,” Zhang says.

