

| Date | 14th, Oct 2022 |
|---|
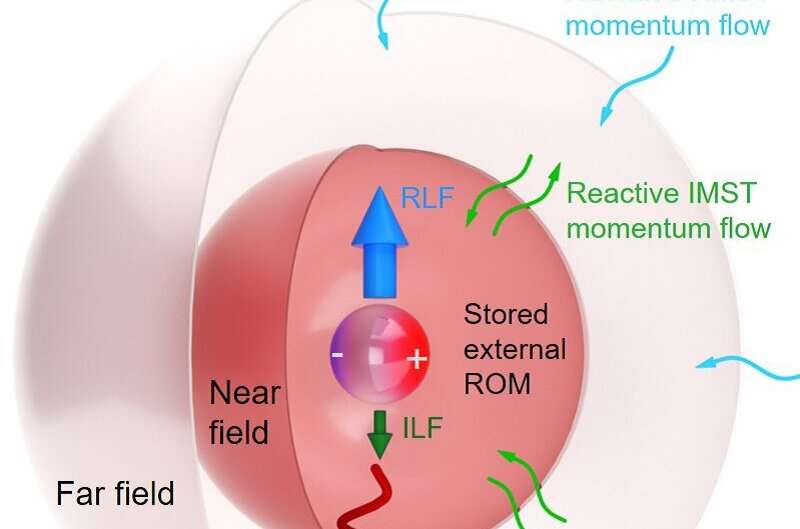 When an electromagnetic wave, (for example a monochromatic plane wave, as illustrated here), impinges on a body, charges are separated, thus inducing multipoles. The object feels a time-averaged Lorentz force, RLF, associated to the field (i.e. Poynting) momentum flux, RMST, flowing into a far-field surface, (e.g. spherical as shown). However, there also appears a flow, IMST, of imaginary field momentum, related to momentum flux going back and forth across a near-field surface, with zero time-average, which accumulates reactive strength of orbital momentum, ROM, stored both inside and in the near-field of the object, and meanwhile yields a reactive force, ILF, on the body. Credit: Manuel Nieto-Vesperinas, Xiaohao Xu
When an electromagnetic wave, (for example a monochromatic plane wave, as illustrated here), impinges on a body, charges are separated, thus inducing multipoles. The object feels a time-averaged Lorentz force, RLF, associated to the field (i.e. Poynting) momentum flux, RMST, flowing into a far-field surface, (e.g. spherical as shown). However, there also appears a flow, IMST, of imaginary field momentum, related to momentum flux going back and forth across a near-field surface, with zero time-average, which accumulates reactive strength of orbital momentum, ROM, stored both inside and in the near-field of the object, and meanwhile yields a reactive force, ILF, on the body. Credit: Manuel Nieto-Vesperinas, Xiaohao Xu
Optical manipulation of matter by using the mechanical action of light is one of the vibrant subjects of micro and nanoscience. In 2018 the Nobel Prize in physics was awarded to Arthur Ashkin for the invention and development of optical tweezers.
The Maxwell stress tensor (MST), which expresses the conservation of linear and angular momentum, is the cornerstone of electromagnetic forces.
When the wavefields are characterized by complex functions, the MST conservation law is obtained from the real parts which yield the currently observed time-averaged Lorentz forces (RLFs) and torques. In this context, it is well-known that the RLF on a volume V of charges and currents is given by the Poynting momentum flux whose density is the real part of the Maxwell stress tensor (RMST) across any contour enclosing V. In consequence this RLF may be considered as the flow, characterized by the RMST, into the surface of a sphere in the far-field, i.e. in the radiation zone of V, and as such, it may be considered a "radiation force".
In a new paper published in Light: Science & Applications, Manuel Nieto-Vesperinas from the Instituto de Ciencia de Materiales de Madrid, CSIC, Spain, and Xiaohao Xu from the State Key Laboratory of Transient Optics and Photonics and Xi'an Institute of Optics and Precision Mechanics, Chinese Academy of Sciences, China, have demonstrated that the theory through the RMST describes only half the physics of the electromagnetic optical force.
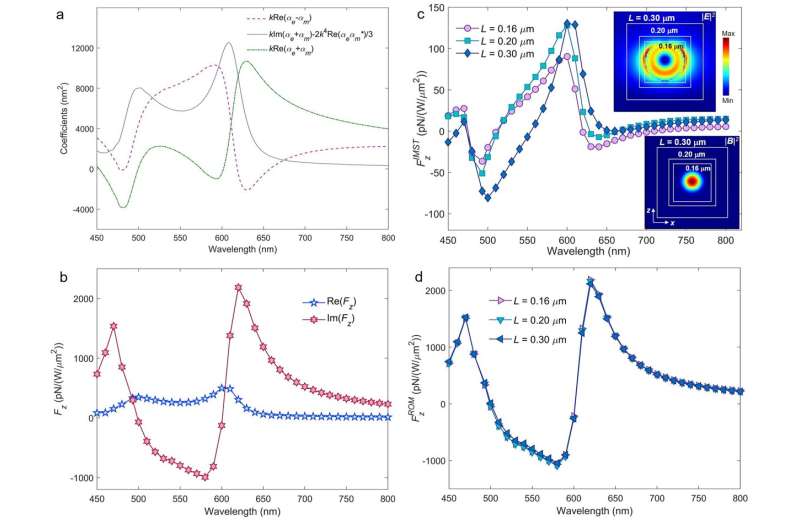 (a) Combined sphere polarizabilities calculated via Mie theory. The expression of the time-averaged radiation pressure < Fz > given by these polarizabilities according to the theory is shown in the full line, while the broken one depicts the theoretical flow IMST, expressed by FIMST which is the z-component of the reactive force, F'z, according to the thory. (b) Numerical results for the time-averaged force < Fz > and reactive force F'z on the sphere. (c) IMST component, FIMST, of the ILF numerically calculated with different cube integration contours. Insets show maps on the x = 0 plane of |E|² and |B|² at wavelength of 610 nm which corresponds to the magnetic dipole resonance. White broken line squares illustrate the integration contours. (d) ROM component, FROM, along OZ , of the ILF calculated by subtracting FIMST from F'z. Credit: Manuel Nieto-Vesperinas, Xiaohao Xu
(a) Combined sphere polarizabilities calculated via Mie theory. The expression of the time-averaged radiation pressure < Fz > given by these polarizabilities according to the theory is shown in the full line, while the broken one depicts the theoretical flow IMST, expressed by FIMST which is the z-component of the reactive force, F'z, according to the thory. (b) Numerical results for the time-averaged force < Fz > and reactive force F'z on the sphere. (c) IMST component, FIMST, of the ILF numerically calculated with different cube integration contours. Insets show maps on the x = 0 plane of |E|² and |B|² at wavelength of 610 nm which corresponds to the magnetic dipole resonance. White broken line squares illustrate the integration contours. (d) ROM component, FROM, along OZ , of the ILF calculated by subtracting FIMST from F'z. Credit: Manuel Nieto-Vesperinas, Xiaohao Xu
The other half, so far ignored, is characterized by the imaginary part of the complex Maxwell stress tensor, related to the exchange of reactive (i.e. imaginary Poynting) momentum, and acquires importance as optical manipulation of matter progresses and expands its scope incorporating reactive concepts. The imaginary Maxwell stress tensor (IMST) builds-up in and around V what they put forward as the reactive strength of orbital (or canonical) momentum (ROM); so that this storage of ROM contributes to what they found as the imaginary Lorentz force (ILF) and imaginary torque on V, which may also be envisaged as a reactive strength of Poynting momentum.
Such a reactive force, ILF, is not observable on time averaging since its net value is zero, but it exists instantaneously due to the exchange of reactive momentum, which alternates with time between the wave and the body. Hence, the ILF is a basically fundamental dynamic phenomenon, inherent to the emergence of electromagnetic and optical forces, being also associated to the appearance of reactive power, reactive work, and reactive helicity. The former having been for many years a well-known workhorse in the design of RF antennas, and recently studied in micro and nano-antennas.
Therefore, like in RF antenna design one aims to diminish the reactive power and reactive work to increase the radiation efficiency, the theory put forward in this paper constitutes a tool to act on the ROM and ILF in order to optimize a desired radiation pressure in optical manipulation. Consequently, it is shown that, as such, the ILF and ROM play an antagonic role with respect to the standard RLF, so that a strong ILF, and thus a large ROM storage, amounts to a loss of radiative force, RLF, and vice-versa. This makes the ROM and ILF indirectly observable.
The authors state that it is somewhat striking that having existed for decades the complex Poynting theorem and its associated reactive quantities: the IPM, reactive work and reactive energy, the complex Maxwell stress tensor theorem, and the reactive entities it conveys, seem to have never been established. Perhaps this being due to the practical difficulties involved in the accurate control of optical manipulation. However the fast advances and present maturity of the optical handling of matter, now warrant their formulation.
From their point of view, this novel scenario completes an interpretative panorama of forces in the science of light and classical electrodynamics, e.g. in the design of particles and of structured beam illumination that, as done with their radiative power and emitted field helicity, the efficiency of the time-averaged force, i.e. of the RLF acting on them, be optimized by either enhancing or weakening it.
More information: Manuel Nieto-Vesperinas et al, The complex Maxwell stress tensor theorem: The imaginary stress tensor and the reactive strength of orbital momentum. A novel scenery underlying electromagnetic optical forces, Light: Science & Applications (2022). DOI: 10.1038/s41377-022-00979-2
Citation: The complex Maxwell stress tensor theorem: A novel scenery underlying electromagnetic optical forces (2022, October 14) retrieved 1 November 2022 from https://phys.org/news/2022-10-complex-maxwell-stress-tensor-theorem.html
This document is subject to copyright. Apart from any fair dealing for the purpose of private study or research, no part may be reproduced without the written permission. The content is provided for information purposes only.
